LinearKAN: A very fast implementation of Kolmogorov-Arnold Networks via Dynamic Input-Indexed Matrix Multiplication

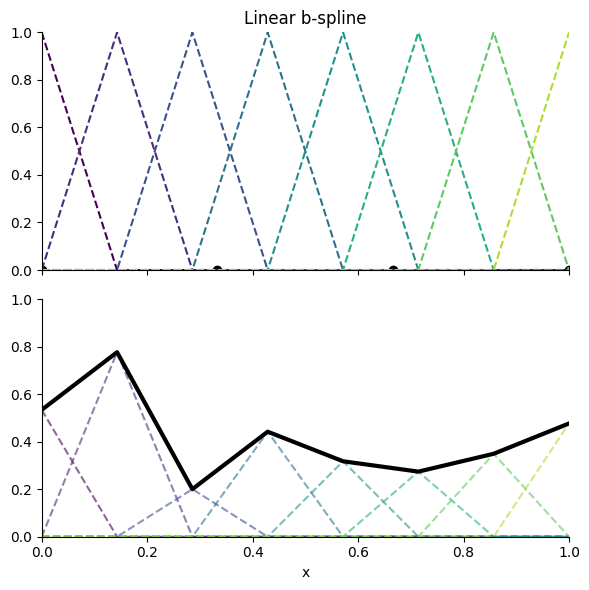
Kolmogorov-Arnold Networks (KANs) training and inference are accelerated by orders of magnitude through exploiting the structure of the uniform linear (C⁰) B-spline (see Fig. 1). Because the intervals are uniform, evaluating spline(x) reduces to a constant-time index calculation, followed by looking up the two relevant control points and linearly interpolating between them. This contrasts with the summation over basis functions typically seen in splines, reducing the amount of computation required and enabling effectively sublinear scaling across the control points dimension.

Going one step further, we reinterpret this lookup interpolation approach as a dynamic input-indexed sparse-dense matrix multiplication (SpMM), squeezing out additional performance through cuSPARSE, a highly optimized CUDA library. This computational approach falls within the framework of conditional computation, albeit at a more granular level compared to Mixture of Experts (MoEs), the most popular form of conditional computation.

Misc

A special version of KAN with "5 control points" can utilize 2:4 semi-structured sparsity acceleration on Ampere and newer NVIDIA architectures. This is a work in progress. See minimal.py to gain a general understanding. This also has potential quantization benefits (untested) as interpolation weights in general are from 0 to 1, and each spline only uses 2 active parameters per sample. This layer can take advantage of NVIDIA paired 4:8 for e2m1, unlocking potential acceleration at low quantization.

Notebook representing KAN as a matrix multiply while being more efficient than MLP

Install

pip install kanditioned

Usage

Important

It is highly recommended to use this layer with torch.compile, which may provide very significant speedups, in addition to a normalization layer before each KANLayer. Custom kernel is coming sometimes later. Stay tuned.

from kanditioned.kan_layer import KANLayer

layer = KANLayer(in_features=3, out_features=3, init="random_normal", num_control_points=8, spline_width=4.0)
layer.visualize_all_mappings(save_path="kan_mappings.png")

Arguments

in_features (int)

Size of each input sample.

---

out_features (int)

Size of each output sample.

---

init (str)

Initialization method:

• "random_normal"

  Each spline initialized to a linear line with its slope drawn from a normal distribution, then normalized so each “neuron” has unit weight norm.

• "identity"

  Each spline initialized to a linear line with slope one (requires in_features == out_features). Output initially equals input.

• "zero"

  Each spline initialized to a linear line with slope zero.

---

num_control_points (int, default = 32)

Number of uniformly spaced control points per input feature.

---

spline_width (float, default = 4.0)

Domain the spline control points are uniformly defined on: [-spline_width / 2, spline_width / 2]. Outside the domain, the spline will linearly extrapolate.

---

impl (str, default = "embedding_bag")

Implementation choice:

• "embedding_bag"

  Much faster for inference with torch.compile enabled, or for either training or inference without torch.compile.

• "embedding"

  Appears to be somewhat faster when training with torch.compile enabled.

Note

Experiment with both to achieve peak performance.

Methods

visualize_all_mappings(save_path: str, optional)

Plots the shape of each spline along with its corresponding input and output feature.

Figure

Figure 1. Linear B-spline example (each triangle-like shape is a basis):

Roadmap (more like TODO list XD)

• Use F.embedding_bag
• Add CSR sparse-dense matmul implementation
• Add dense matmul version
• Add 2:4 semi-structured sparsity version for num_control_points = 5
• Investigate swapping the linear layer with KAN to increase capacity without retraining
• Check out other sparse storage formats for sparse matmul
• Add support for index select with lerp implementation and investigate index_add
• Update doc for variant and other new parameters introduced
• Support sparse gradients
• Update package with cleaned up, efficient Discrete Cosine Transform (with rank-2 correction) and parallel scan (prefix sum) parameterizations.
  • Both provide isotropic O(1) condition scaling for the discrete second difference penalty, as opposed to O(N^4) conditioning for the naive B-spline parameterization. This only matters if you care about regularization.
  • May add linearDCT variant first. Although it's O(N^2), it's more parallelized and optimized on GPU for small N since it's essentially a matmul with weight being a DCT matrix
• Proper baselines against MLP and various other KAN implementations on backward and forward passes
• Add sorting on indices and unsorting as an option (potentially radix sort, which is common optimization on embedding) to improve computational time through global memory "coalesced" access
• Add in feature-major input variant
• May change to either unfold or as_strided (slight performance improvement)
• Benchmark against NanoGPT
• Make announcements on various platforms
• Run benchmarks and further optimize memory locality
  • Feature-major input variant versus batch-major input variant
  • Interleaved indices [l1, u1, l2, u2, ...] versus stacked indices [l1, l2, ..., u1, u2, ...]
• Add optimized Triton kernel
• Update visualize_all_mappings method to something like .plot with option for plotting everything
• Add a nice-looking figure
• Add autograd backward impl. in
• Check out https://github.com/NVIDIA/cuEmbed
• Research adding Legendre polynomials parameterization
  • Preliminary: does not seem to offer many benefits or have isotropic penalty conditioning
• Experiment with input bucketing instead of index-based calculation (torch.bucketize)
• Add similar papers in
• Polish writing

Open To Collaborators. Contributions Are Welcomed!

LICENSE

This project is licensed under the Apache License 2.0.